The Continuous 48.6 dB(A) Equivalence (FERC Part 2)

Have you ever come across a statement like the following and wondered what it meant exactly?

The FERC noise regulation limits compressor station noise contributions to no more than 55 dB(A) day-night average (L_dn) or equivalently, no more than a continuous 48.6 dB(A) at the surrounding noise sensitive areas (NSAs) such as schools, hospitals, or residences.

Perhaps you saw it in a FERC Resource Report 9 or some other filing. For this post, I want to show you the meaning behind the phrase "…or equivalently, no more than a continuous 48.6 dB(A)."

In Part1, we learned that the L_dn metric has an extra 10 decibels added to measured sound levels occurring during nighttime hours (10 pm - 7 am). The L_dn is a weighted average embedded inside a logarithm, which makes it difficult to get a feel for. Let's set that +10 penalty aside for a moment to make it easier to think about.

We will start by thinking of a sound source that is steady; emitting the same sound level all the time, without fail or interruption. Let's further say that sound source is in an isolated location, so that it is the only sound source around. Say that sound level is 60 dB(A) for example. Since the sound level is 60 dB(A) all the time, then the average sound level over any time period (whether 5 minutes, 1 hour, 24 hours, etc.) would be 60 dB(A). During the 15 hours of daytime, the sound level is always 60 dB(A), so the daytime average sound level, L_d, is 60 dB(A). Similarly, the nighttime average sound level, L_n, is also 60 dB(A).

So what happens when the +10 nighttime penalty comes into play and we want to know what the L_dn would be for this steady sound? Let's revisit the definition of L_dn from Part 1:

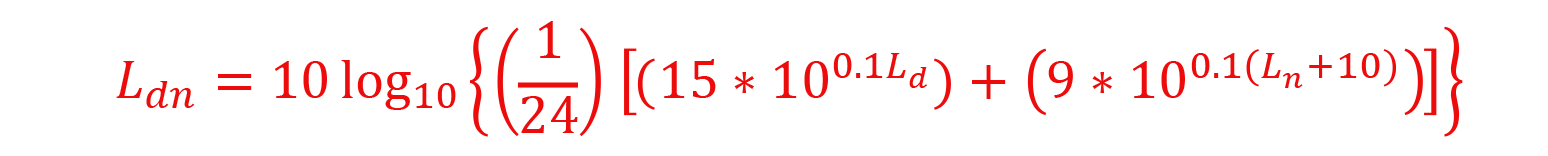
From here, we can proceed two ways, either set Ld = Ln = 60 dB(A) (assuming the same value as before) and calculate the result, which is 66.4 dB(A) L_dn. Or set L_d = L_n and have some math fun using the properties of logarithms to reduce it to the following:

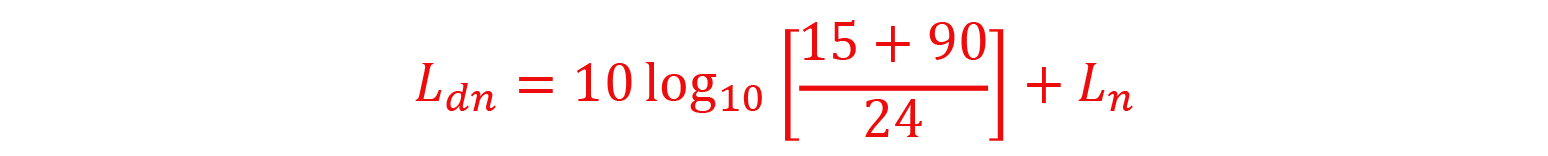
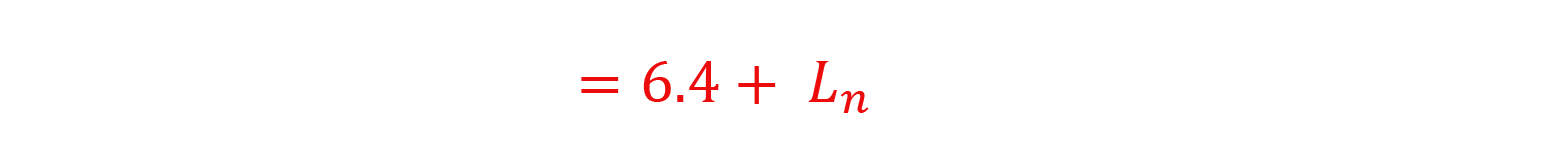
Whichever path you take, you can see that when the daytime and nighttime average sound levels are equal, the resulting L_dn is 6.4 greater.

If a sound source is steady, that is, continuously emitting the same sound day and night, then the L_dn is 6.4 dB(A) greater than whatever the sound level meter would read at any given moment.

We can turn this around to find out what the continuous sound level equivalent to our FERC limit would be. Knowing that our L_dn limit is 55 dB(A), then we can determine that 55 - 6.4 = 48.6 dB(A) would be the limit for a steady, continuous sound.

We just learned:

• A "continuous sound of x dB(A)" is equivalent to "x + 6.4 dB(A) L_dn."
• ‘48.6 dB(A) continuous’ + 6.4 = 55 dB(A) L_dn .
• 55 dB(A) L_dn is equivalent to a continuous 48.6 dB(A).

About the Author - Tim Simmons, Ph.D. - USSI Director of Industrial Acoustics
Dr. Tim Simmons manages USSI's Industrial Acoustics Department. Tim comes to USSI with a wealth of Acoustical and Noise Control knowledge and real-world experience. Tim holds a Ph.D. in Physics from the University of Mississippi and a B.S. in Engineering Physics from the University of Tennessee.
Member INCE, ASA, ASME